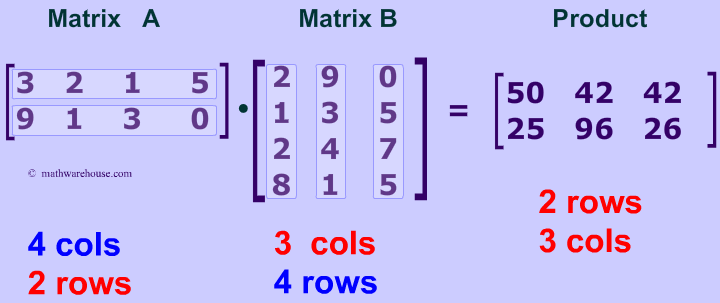
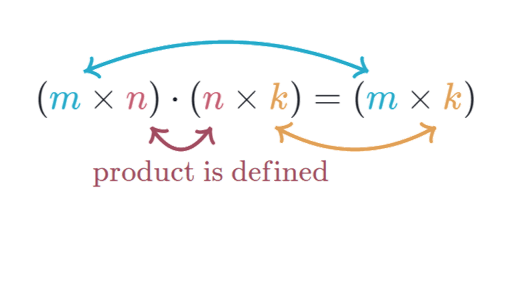Finding The Dimensions Of A Matrix

For example if a is a 3 by 4 matrix then size a returns the vector 3 4. Google classroom facebook twitter. With help of this calculator you can.

flat roof maintenance paint floral coolers for lease faux polar bear rug flowers in the attic movie true story faze rug haunted video flexible solar panel durability forward solar roofing review flexispot electric standing desk

Dimensions Of A Matrix Youtube

Matrix Multiplication Dimensions Article Khan Academy

Linear Algebra Example Problems Matrix Column Space Basis And Dimension Youtube

Ex Determine The Dimensions And Elements Of A Matrix Youtube

Mathwords Element Of A Matrix

Adding And Subtracting Matrices Chilimath

Matrix multiplication dimensions learn about the conditions for matrix multiplication to be defined and about the dimensions of the product of two matrices.

Finding the dimensions of a matrix.

Find the matrix determinant the rank raise the matrix to a power find the sum and the multiplication of matrices calculate the inverse matrix. Since a has three rows and four columns the size of a is 3 4 pronounced as three by four. For instance consider the following matrix a. The dimension is the number of bases in the column space of the matrix representing a linear function between two spaces.

If a is a table or timetable then size a returns a two element row vector consisting of the number of rows and the number of table variables. Just type matrix elements and click the button. This means that a has m rows and n columns. The dimensions for a matrix are the rows and columns rather than the width and length.

A matrix with m rows and n columns is called an m n matrix or m by n matrix while m and n are called its dimensions. But this is just a little reminder and not actually part of the matrix. Leave extra cells empty to enter non square matrices. The numbers of rows and columns of a matrix are called its dimensions.

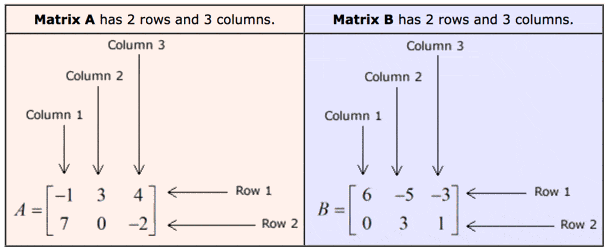
Sometimes the dimensions are written off to the side of the matrix as in the above matrix. Here is a matrix with three rows and two columns. The dimensions of a matrix a are typically denoted as m n. For example the matrix a above is a 3 2 matrix.

The columns go up and down. Sz size a returns a row vector whose elements are the lengths of the corresponding dimensions of a. When referring to a specific value in a matrix called an element a variable with two subscripts is often used to denote each element based on their position in the matrix. The size of a matrix is defined by the number of rows and columns that it contains.

If you have a linear function mapping r3 r2 then the column space of the matrix representing this function will have dimension 2 and the nullity will be 1. The rows go side to side.